KAN网络改进NOTEARS算法的思路、动机及解决方案
引言
NOTEARS(Non-combinatorial Optimization via Trace Exponential and Augmented lagRangian for Structure learning)是一种用于从观测数据中学习有向无环图(DAG)的连续优化算法,主要针对线性结构方程模型(SEM)。其非线性扩展NOTEARS-MLP使用多层感知器(MLP)来建模非线性关系。Kolmogorov-Arnold Networks(KAN)作为一种新型神经网络架构,可以替换NOTEARS-MLP中的MLP,提供更好的解释性、准确性和参数效率。
NOTEARS算法简介
NOTEARS将DAG学习转化为连续优化问题,通过最小化损失函数并使用平滑的无环约束:
在非线性版本NOTEARS-MLP中,使用MLP建模每个变量的非线性函数 \( f_j \),扩展为非线性SEM。
KAN网络的动机
KAN基于Kolmogorov-Arnold表示定理,该定理表明任何多变量连续函数可以分解为单变量连续函数的有限组合:
\[f(x_1, \dots, x_n) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^n \phi_{q,p}(x_p) \right)\]
动机包括:
- 改进解释性:KAN的激活函数在边上,是可学习的单变量函数,便于可视化和符号拟合,帮助科学家重新发现数学和物理定律。
- 更高的准确性:较小的KAN在函数拟合和PDE求解中可达到或超过较大MLP的准确性,具有更快的神经缩放律。
- 参数效率:通过B-spline参数化激活函数,减少参数数量,同时保持强大表达能力。
- 应用于因果发现:在NOTEARS的非线性扩展中,KAN可替换MLP建模非线性SEM,提高模型的解释性和性能。
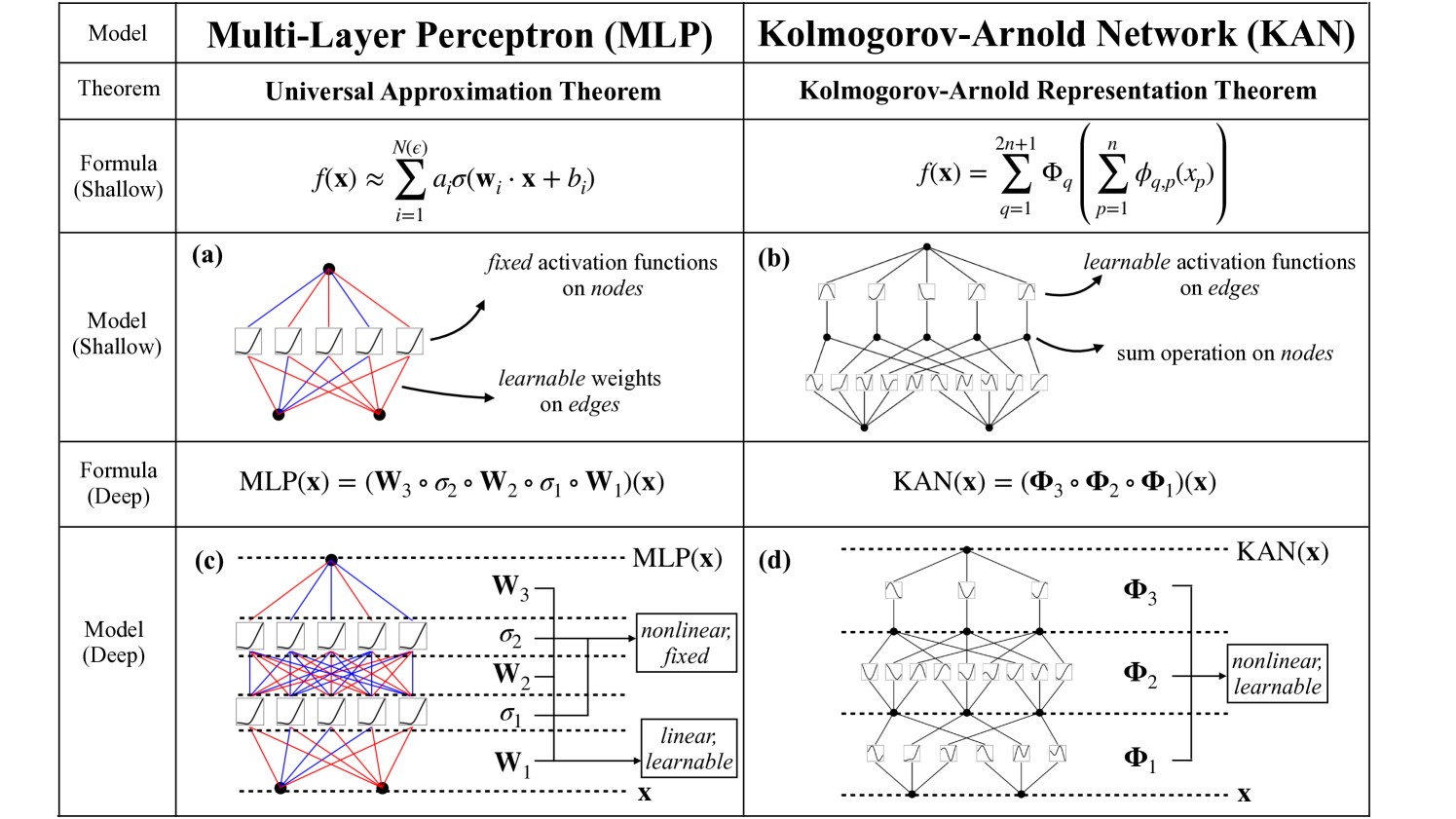
KAN改进NOTEARS的思路
在NOTEARS-MLP中,非线性关系由MLP建模。KAN的思路是使用KAN替换这些MLP:
- 每个变量的函数 \( f_j \) 用KAN表示,利用其单变量激活函数的组合来捕捉复杂非线性。
- 保持NOTEARS的连续优化框架,但受益于KAN的解释性,便于分析因果关系。
- 通过剪枝和符号回归,KAN可以产生稀疏、可解释的DAG。
这解决了NOTEARS-MLP中MLP的黑箱问题,并可能提高在非线性数据上的结构学习准确性。

解决方案
实现步骤:
- 使用B-spline参数化KAN的激活函数:\(\phi(x) = \sum c_i B_i(x)\),其中 \( B_i \) 是B-spline基函数。
- 在NOTEARS框架中,将非线性模型改为KAN:\( X_j = f_j(X_{pa(j)}) + Z_j \),其中 \( f_j \) 是KAN。
- 优化:最小化重构损失,加上无环约束和正则化。使用梯度下降训练KAN参数。
- 后处理:剪枝KAN以获得稀疏DAG,并可选拟合符号公式以增强解释性。
\[L = \frac{1}{n} \sum \|X - f(X, \theta)\|^2 + \lambda h(W(\theta))\]
这解决了非线性因果发现中的解释性和效率问题。

